Pi Facts, page 3
An Indian Approximation of Pi
Here's a riddle recently e-mailed to me by someone named Narayanaswamy in New
Dehli, India:
Question: Place four eights (and no other numbers) in a formula that approximates
pi. For bonus points, break the formula down to yield the same approxmation using
seven twos.
Answer: One of Ramanujan's modular functions yields the following in its first
term:
8.88 /sqrt(8). Bonus answer: (2.22+2.22)/sqrt(2)
Pi in the Royal Air Force
In 1915, pi was adopted as the official symbol for the No. 22 Squadron Royal Flying Corp., R.A.F..
Smells like Pi to Me
Givenchy Pi Neo:

Pi and the Length of Rivers
From Fermat's Enigma, by Simon Singh
"Professor Hans-Henrik Stolum, an earth scientist at Cambridge University has calculated the ratio between the actual length of rivers from source to mouth and their direct length as the crow flies. Although the ratio varies from river to river, the average value is slightly greater than 3, that is to say that the actual length is roughly three times greater than the direct distance. In fact the ratio is approximately 3.14, which is close to the value of the number pi... The ratio of pi is most commonly found for rivers flowing across very gently sloping planes, such as those found in Brazil or the Siberian tundra."
Barbier's Theorem
If you put a circle between two lines and rotate it, it always has the same width, right? There are other shapes that do this, too. For instance, take an equalateral triangle and draw 3 arcs from each corner to the other, with the center at the third corner. The resulting shape is called a Reulaux triangle, and it is a curve of constant width. That is, as you rotate it, it always retains the same width. Barbier's Theorem states that all curves of a constant width have the same perimeter: multiply the constant width by pi. For a circle, you get the circumference by multiplying the diameter of the circle by pi. In a Reuleaux triangle, you would multiply the length of one side of the original triangle. Thanks to Professor Millie Johnson at Western Washington University for this one!
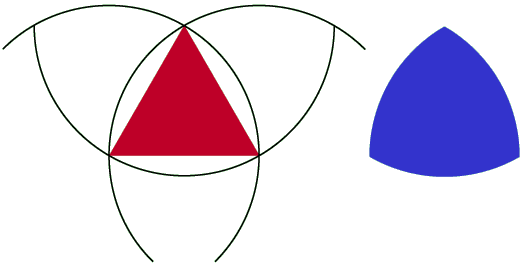
See this page for more information on Reulaux triangles, including some great photos of two British coins based on the shape.

